算法学习笔记

洛谷算法题：

P5705 【深基2.例7】数字反转

题目描述

输入一个不小于 100且小于 1000，同时包括小数点后一位的一个浮点数，例如 123.4 ，要求把这个数字翻转过来，变成 4.321 并输出。

输入格式

一行一个浮点数

输出格式

一行一个浮点数

输入输出样例 #1

输入 #1

1

123.4

输出 #1

1

4.321

解释：

使用scanf输入使用printf打印输出可以快速提高时间，这是因为scanf是C语言的函数，直接调用系统进行I/O操作，而cin是C++的流输入，默认情况下与stdin保持同步，导致有额外的开销。

P5706 【深基2.例8】再分肥宅水

题目描述

现在有 t 毫升肥宅快乐水，要均分给 n 名同学。每名同学需要 2 个杯子。现在想知道每名同学可以获得多少毫升饮料（严格精确到小数点后 3 位），以及一共需要多少个杯子。

输入格式

输入一个实数 $t$ 和一个正整数 n，使用空格隔开。

输出格式

输出两行。 第一行输出一个三位小数，表示可以获得多少毫升饮料。第二行输出一个正整数，表示一共需要多少个杯子。

输入输出样例 #1

输入 #1

1

500.0 3

输出 #1

1
2

166.667
6

说明/提示

对于所有数据，0< t<10000 且小数点后不超过 3 位，1< n< 1000。

解析：

第一种需要用到两个头文件，即 <iostream>（用于提供流输出操作）和 <iomanip>（用于提供保留小数位数的操作）。一般形式为：

1

std::cout << std::fixed << std::setprecision(3) << k;

其中 k 是需要输出的数。 第二种做法用到 <cstdio>（是从 C 语言的 <stdio.h> 继承而来的，提供了 printf 的输出操作），一般形式为：

1

printf("%.3lf", k);

其中 k 也是需要输出的数。 注意，使用 %.3lf 的格式会认为 k 是 double 类型，如果是 float 的话，应当使用 %.3f。

新知：

学会使用头文件中的setprecision可以设置浮点数的输出精度。

C++ 显示多位有效数字

在 C++ 中，可以使用 头文件中的 setprecision 和 fixed 操作符来控制浮点数的输出精度，从而显示指定的有效数字或小数位数。 示例：保留 10 位有效数字 以下代码展示了如何使用 setprecision 设置输出为 10 位有效数字：

1
2
3
4
5
6
7
8
9
10
11
12
13

#include <iostream>

#include <iomanip> // 包含操纵符头文件

int main() {

double pi = 3.141592653589793;

std::cout << std::setprecision(10) << pi << std::endl; // 输出 10 位有效数字

return 0;

}

输出结果：

1

3.141592654

示例：保留小数点后 5 位 如果需要固定小数点后几位，可以结合 fixed 使用：

1
2
3
4
5
6
7
8
9
10
11
12
13

#include <iostream>

#include <iomanip>

int main() {

double value = 123.456789;

std::cout << std::fixed << std::setprecision(5) << value << std::endl; // 小数点后保留 5 位

return 0;

}

输出结果： 123.45679 使用fixed函数用于控制浮点数的输出格式

P5708 【深基2.习2】三角形面积

题目描述

一个三角形的三边长分别是 a、b、c，那么它的面积为 $$ sqrt{p(p-a)(p-b)(p-c)} $$ ，其中 $$ p=frac{1}{2}(a+b+c) $$ 。输入这三个数字，计算三角形的面积，四舍五入精确到 $1$ 位小数。

输入格式

第一行输入三个实数 a,b,c，以空格隔开。

输出格式

输出一个实数，表示三角形面积。精确到小数点后 $1$ 位。

输入输出样例 #1

输入 #1

1

3 4 5

输出 #1

1

6.0

说明/提示

数据保证能构成三角形，0< a,b,c< 1000，每个边长输入时不超过 2 位小数。

新知：

double类型取模

对于整数来说，取模操作相对简单。但对于浮点数，尤其是double类型，取模操作需要特别处理。

方法一：使用内置函数fmod()

C标准库中的math.h头文件提供了一个名为fmod()的函数，专门用于计算浮点数的取模。其原型如下：

1

double fmod(double numerator, double denominator);

这个函数返回numerator除以denominator的余数。如果denominator为0，则fmod()的行为是未定义的。

方法二：手动计算取模

除了使用fmod()函数外，我们还可以手动实现取模操作。以下是一个手动计算double类型取模的示例：

1
2
3
4
5
6
7

double mod(double a, double b) {
    double result = a - (int)(a / b) * b;
    if (result < 0) {
        result += b;
    }
    return result;
}

**sqrt()**函数计算算数平方根

在 C++ 中，开根函数 sqrt() 用于计算一个数的平方根。该函数定义在 头文件中，并且可以处理不同类型的参数，包括 double_、_float 和 _long double_。如果传递负参数给 sqrt() 函数，会发生错误。

P5707 【深基2.例12】上学迟到

题目描述

学校和 yyy 的家之间的距离为 s 米，而 yyy 以 v 米每分钟的速度匀速走向学校。 在上学的路上，yyy 还要额外花费 10 分钟的时间进行垃圾分类。 学校要求必须在上午 8:00 到达，请计算在不迟到的前提下，yyy 最晚能什么时候出门。 由于路途遥远，yyy 可能不得不提前一点出发，但是提前的时间不会超过一天。

输入格式

一行两个正整数 _s,v_，分别代表路程和速度。

输出格式

输出一个 24 小时制下的时间，代表 yyy 最晚的出发时间。 输出格式为 HH:MM，分别代表该时间的时和分。必须输出两位，不足前面补 $0$。

输入输出样例 #1

输入 #1

1

100 99

输出 #1

1

07:48

说明/提示

对于100%的数据，1 <s,v < 10000。

新知：

时间表示

如何用条件语句描述24小时制的时间

ceil()函数

ceil()函数用于返回大于或等于给定数值的最小整数值，即向上取整。这个函数在数学和工程中常被用于向上取整操作。 位于cmath头文件中使用时要加上

1

#include <cmath>

B2029 大象喝水

题目描述

一只大象口渴了，要喝 20升水才能解渴，但现在只有一个深 h 厘米，底面半径为r 厘米的小圆桶 （h 和r 都是整数）。问大象至少要喝多少桶水才会解渴。 这里我们近似地取圆周率 pi =3.14

输入格式

输入有一行：包行两个整数，以一个空格分开，分别表示小圆桶的深 $h$ 和底面半径 $r$，单位都是厘米。

输出格式

输出一行，包含一个整数，表示大象至少要喝水的桶数。

输入输出样例 #1

输入 #1

1

23 11

输出 #1

1

3

数据规模与约定

对于全部的测试点，保证 1 <h < 500，1 < r <100。

新知：C/C++语言有以下几种取整方法：

1、直接赋值给整数变量。如： int i = 2.5; 或 i = (int) 2.5; 这种方法采用的是舍去小数部分。 2、C/C++中的整数除法运算符”/“本身就有取整功能(int / int)，而下面介绍的取整函数返回值是double。整数除法对正数的取整是舍去小数部分，但是整数除法对负数的取整结果和使用的C编译器有关。 3、使用floor函数。floor(x)返回的是x的整数部分，即小于等于x的最大整数。如： floor(2.5) = 2 floor(-2.5) = -3 4、使用ceil函数。ceil(x)返回的是大于等于x的最小整数。如： ceil(2.5) = 3 ceil(-2.5) = -2 5、round(x)返回x的四舍五入整数值。

宁波oj ：1122. 百灯判熄

描述:

有M盏灯，编号为1~M，分别由相应的M个开关控制。开始时全部开关朝上（朝上为开，灯亮），然后进行以下操作：编号凡是1的倍数的灯反方向拨一次开关；是2的倍数的灯再反方向拨一次开关；是3的倍数的灯又反方向拨一次开关，……，直到是M的倍数的灯又反方向拨一次开关。请从键盘输入一个整数m代表灯的数量，求出最后为熄灭状态的灯（不亮）的数量以及编号并输出。

输入:

输入一个整数m(1≤m≤100)。

输出:

输出为两行，第一行是熄灭状态的灯的数量;第二行是最后为熄灭状态的灯的编号（每个数据以4列的域宽显示）。

例子:

输入:

1

100

正确输出:

1
2

10
   1   4   9   16   25   36   49   64   81 100

提示:

输出控制为%4d 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#include <stdio.h>

int main() {
    int m;
    // 读取输入的灯的数量
    scanf("%d", &m);

    // 声明数组存储灯的状态，1表示亮，0表示灭
    // 索引0不用，从1开始
    int lights[101] = {0}; // 因为m≤100，所以数组大小101足够

    // 初始化所有灯为亮的状态
    for (int i = 1; i <= m; i++) {
        lights[i] = 1;
    }

    // 模拟开关操作
    for (int i = 1; i <= m; i++) {
        // 对i的倍数的灯进行一次开关操作
        for (int j = i; j <= m; j += i) {
            lights[j] = !lights[j];  // 状态取反
        }
    }

    // 统计并收集熄灭的灯的编号
    int count = 0;
    int off_lights[100]; // 存储熄灭的灯的编号

    for (int i = 1; i <= m; i++) {
        if (lights[i] == 0) {
            off_lights[count++] = i;
        }
    }

    // 按要求格式输出结果
    printf("%dn", count);
    for (int i = 0; i < count; i++) {
        printf("%4d", off_lights[i]);
    }
    printf("n");

    return 0;
}

1033. 计算最高位数字

描述:

输入一个任意长度的非负整数，求出其最高位数字。如，输入237，则最高位数字为2。

输入:

输入一个非负整数。

输出:

输出最高位数字

例子:

输入:

1

4756

正确输出:

1

4

代码

1
2
3
4
5
6
7
8
9
10
11

#include <stdio.h>

int main() {
    int n,g;
    scanf("%d", &n);
    while(n>=10) {
        n=n/10;
    }
    printf("%d",n);
    return 0;
}

1050. 字符个数统计

描述:

从键盘输入一行字符，统计字符的个数。输入以换行符结束。

输入:

输入一行字符，以换行符作为结束标记。

输出:

统计字符的个数并输出。不包括换行符。

例子:

输入:

1

Hello Boy.

正确输出:

1

10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

#include <stdio.h>

int main() {
    char c;
    int i =0;
    while (scanf("%c", &c) ==1) {
        if (c == 'n') {
            break;
        }
        i++;
    }
    printf("%dn", i);

    return 0;
}

1054. 相邻字符判相等

描述:

输入一行字符（长度小于等于1000），判断其中是否存在相邻两个字符相同的情形，若有，则输出该相同的字符并结束程序(只需输出第一种相等的字符即可)。否则输出No。

输入:

输入一行字符（长度小于等于1000）

输出:

若有相邻字符相等则输出该相同的字符，否则输出No。（只需要输出第一种相同的情况即可）

例子:

输入:

1

hello anna

正确输出:

1

l

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include <stdio.h>

int main() {
    char s = '�';
    char c;     
    int count = 0;    

    // 读取第一个字符
    if (scanf("%c", &s) != 1) {
        printf("Non");
        return 0;
    }
    count++;

    while (count < 1000 && scanf("%c", &c) == 1) {
        if (c == 'n') {
            break;
        }
        if (c == s) {
            printf("%cn", c);
            return 0;
        }
        s = c;
        count++;
    }
    printf("Non");
    return 0;
}

126. 水仙花数

描述:

输入整数n，求小于n的水仙花数（n<1000）。所谓“水仙花数”是指一个三位正整数ABC，其各位数字的立方和等于该数本身，即 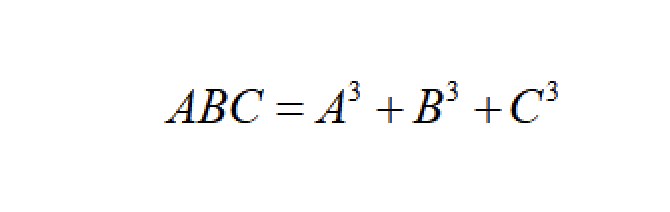例如，370是一个水仙花数，因为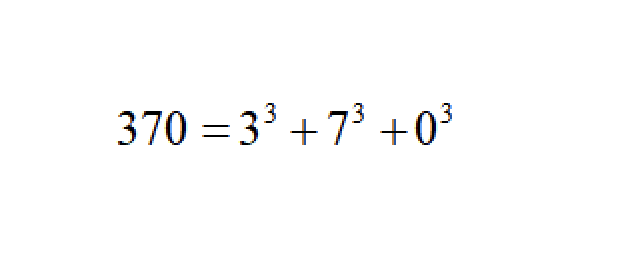

输入:

输入一个正整数n(n<1000)

输出:

输出小于n的所有水仙花数。如果该范围内部不存在水仙花数，则输出No Answer。

例子:

输入:

1

400

正确输出:

1
2
3

153
370
371

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

#include <stdio.h>

int main() {
int n,b,s,g,count=0;
    int arr[1000];
    scanf("%d", &n);
    for (int i = 100; i < n; i++) {
        b =i/100%10;
        s = i/10%10;
        g = i%10;
        if(i == b*b*b+s*s*s+g*g*g) {
            printf("%dn",i);
            count++;
        }

    }
    if(count ==0) {
        printf("No Answer");
    }
    return 0;
}

1130. 判断素数

描述:

输入一个整数n（n>1），判断其是否为素数。素数的定义为：一个大于1的整数，如果除了1和其自身以外没有其他正因子，则称此数为素数或质数。

输入:

输入一个整数n(n>1)。

输出:

如果该数是素数就输出yes，如果不是就输出no。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include <stdio.h>
#include <math.h>

int main() {
    int n;
    scanf("%d", &n);

    // 假设是素数
    int is_prime = 1;

    // 素数判断：检查从2到sqrt(n)的所有数是否能整除n
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) {
            // 找到因子，不是素数
            is_prime = 0;
            break;
        }
    }

    // 输出结果
    if (is_prime) {
        printf("yesn");
    } else {
        printf("non");
    }

    return 0;
}

拓展：

输入一个整数，给我输出1到这个整数范围内所有的质数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

#include <stdio.h>
#include <math.h>

// 判断一个数是否为质数
int isPrime(int num) {
    if (num <= 1) {
        return 0; // 1 不是质数
    }
    if (num == 2) {
        return 1; // 2 是质数
    }
    if (num % 2 == 0) {
        return 0; // 偶数（除 2 外）不是质数
    }
    // 只需判断到 sqrt(num) 即可，减少计算量
    for (int i = 3; i <= sqrt(num); i += 2) {
        if (num % i == 0) {
            return 0;
        }
    }
    return 1;
}

int main() {
    int n;
    printf("请输入一个整数：");
    scanf("%d", &n);

    if (n < 2) {
        printf("该范围内没有质数n");
    } else {
        printf("1到%d范围内的质数有：n", n);
        for (int i = 2; i <= n; i++) {
            if (isPrime(i)) {
                printf("%d ", i);
            }
        }
        printf("n");
    }

    return 0;
}

1132. 最大公约数和最小公倍数

描述:

求两个正整数的最大公约数和最小公倍数。

输入:

输入两个正整数。

输出:

输出最大公约数与最小公倍数。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#include <stdio.h>

int main() {
    int a, b, num1, num2, temp;

    scanf("%d %d", &num1, &num2);

    a = num1;
    b = num2;

    while (b != 0) {
        temp = b;
        b = a % b;
        a = temp;
    }
    int gcd = a;

    int lcm = (num1 / gcd) * num2;

    printf("%d %dn", gcd, lcm);

    return 0;
}

1166. 稀疏字母金字塔（1）

描述:

从键盘输入一个整数n，输出n行的字母金字塔。如下图所示的是一个n为6的字母金字塔。

输入:

输入一个整数n。

输出:

输出n行的字母金字塔。

例子:

输入:

1

6

正确输出:

1
2
3
4
5
6

     A
    B B
   C C C
  D D D D
 E E E E E
F F F F F F

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include <stdio.h>

int main() {
    int n;
    scanf("%d", &n);

    for (int i = 1; i <= n; i++) {
        // 打印每行前面的空格
        for (int j = 1; j <= n - i; j++) {
            printf(" ");
        }
        // 打印当前行的字母（带空格分隔）
        char letter = 'A' + i - 1;
        for (int k = 1; k <= i; k++) {
            printf("%c", letter);
            // 字母间加空格（最后一个字母后不加）
            if (k < i) {
                printf(" ");
            }
        }
        printf("n"); // 换行
    }

    return 0;
}

1174. 哥德巴赫猜想(难☹️)

描述:

所谓哥德巴赫猜想是指，任一大于2的偶数都可以写成两个质数之和（严格说来，这是欧拉的等价描述版本）。例如6=3+3,8=3+5，…，18=7+11。迄今为止，这仍然是一个著名的世界难题，被誉为数学王冠上的明珠。试编写程序，验证任一大于2的偶数都能写成两个质数之和。（可能有多种情况，请输出两数差最大的那组）

输入:

输入一个大于2的偶数N。

输出:

输出两个质数和的形式，小的质数在前,大的质数在后。

例子:

输入:

1

16

正确输出:

1

16=3+13

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

#include <stdio.h>
#include <math.h>

int main() {
    int N;
    scanf("%d", &N);

    int min_p, max_p;
    int max_diff = -1;

    // 遍历可能的第一个质数（从2到N/2）
    for (int i = 2; i <= N / 2; i++) {
        // 判断i是否为质数
        int is_i_prime = 1;
        if (i <= 1) {
            is_i_prime = 0;
        } else if (i == 2) {
            is_i_prime = 1;
        } else if (i % 2 == 0) {
            is_i_prime = 0;
        } else {
            for (int j = 3; j <= sqrt(i); j += 2) {
                if (i % j == 0) {
                    is_i_prime = 0;
                    break;
                }
            }
        }

        if (is_i_prime) {
            int j = N - i;  // 计算另一个数
            // 判断j是否为质数
            int is_j_prime = 1;
            if (j <= 1) {
                is_j_prime = 0;
            } else if (j == 2) {
                is_j_prime = 1;
            } else if (j % 2 == 0) {
                is_j_prime = 0;
            } else {
                for (int k = 3; k <= sqrt(j); k += 2) {
                    if (j % k == 0) {
                        is_j_prime = 0;
                        break;
                    }
                }
            }

            // 若两数都是质数，计算差值并更新最大差值组合
            if (is_j_prime) {
                int diff = j - i;
                if (diff > max_diff) {
                    max_diff = diff;
                    min_p = i;
                    max_p = j;
                }
            }
        }
    }

    printf("%d=%d+%dn", N, min_p, max_p);
    return 0;
}

1213. 判断亲密数

描述:

如果整数A的全部因子(包括1,不包括A本身)之和等于B,并且整数B的全部因子（包括1，不包括B本身）之和等于A，则称整数A和B为亲密数。任意输入两个正整数，判断他们是否为亲密数。若是亲密数，则输出1，否则输出0.

输入:

输入两个整数。

输出:

若是亲密数，则输出1，否则输出0。

例子:

输入:

1

220 284

正确输出:

1

1

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#include <stdio.h>

int main() {
    int a, b;
    int sum_a = 0;  // 存储a的真因子之和
    int sum_b = 0;  // 存储b的真因子之和

    scanf("%d%d", &a, &b);

    // 计算a的所有真因子（不包括a本身）之和
    for (int i = 1; i < a; i++) {
        if (a % i == 0) {  // i是a的真因子
            sum_a += i;
        }
    }

    // 计算b的所有真因子（不包括b本身）之和
    for (int i = 1; i < b; i++) {
        if (b % i == 0) {  // i是b的真因子
            sum_b += i;
        }
    }

    // 判断是否为亲密数：sum_a等于b且sum_b等于a
    if (sum_a == b && sum_b == a) {
        printf("1");
    } else {
        printf("0");
    }

    return 0;
}

1222. 表示成两个数的平方和

描述:

输入一个正整数N，找出所有满足X^2+Y^2=N的正整数对X和Y。

输入:

输入一个正整数N。

输出:

输出这两个正整数X和Y，满足X^2+Y^2=N，输出时要求X<=Y。如果无解则不需要输出任何信息。

例子:

输入:

1

50

正确输出:

1
2

1 7
5 5

提示:

当有多组输出时,按照X从小到大的顺序排列。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

#include <stdio.h>
#include <math.h>

int main() {
    long long N;
    scanf("%lld", &N);

    // 从1到sqrt(N/2)遍历X
    for (long long X = 1; X * X <= N / 2; X++) {
        long long Y_squared = N - X * X;
        long long Y = (long long)sqrt(Y_squared);

        // 检查Y是否为整数且X<=Y
        if (Y * Y == Y_squared && X <= Y) {
            printf("%lld %lldn", X, Y);
        }
    }

    return 0;
}

1211. 还是鸡兔同笼

描述:

一个笼子里面关了鸡和兔子（鸡有2只脚，兔子有4只脚）。已经知道了笼子里面脚的总数a，问笼子里面至少有多少只动物，至多有多少只动物。

输入:

第一行是测试数据的组数n，后面跟着n行输入。每组测试数据占一行，每行包含一个正整数a，代表笼子里面脚的总数。

输出:

输出包含n行，每行对应一个输入，包含2个正整数，第一个是最少的动物数，第二个是最多的动物数。如果没有满足要求的答案，则输出两个0。

例子:

输入:

1
2
3

2
3
20

正确输出:

1
2

0 0
5 10

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include <stdio.h>

int main() {
    int n, a;
    scanf("%d", &n);

    while (n--) {
        scanf("%d", &a);

        // 判断是否有解（脚的总数必须是偶数）
        if (a % 2 != 0) {
            printf("0 0n");
        } else {
            // 计算最少动物数
            int min = (a + 2) / 4;
            // 计算最多动物数
            int max = a / 2;

            printf("%d %dn", min, max);
        }
    }

    return 0;
}

解析：最少动物数 = (a+2)/4 的由来

情况 1：a 能被 4 整除（a=4k，k 为整数）

代入 (a + 2) / 4： (4k + 2) / 4 = k + 2/4 → 整数除法后结果为 k（丢弃小数 0.5），恰好等于 a/4（4k/4=k）。 例：a=20（4×5）→ (20+2)/4=22/4=5.5 → 整数除法得 5，和 20/4=5 一致。

情况 2：a 不能被 4 整除（a=4k+2，k 为整数，因 a 是偶数）

代入 (a + 2) / 4： (4k + 2 + 2) / 4 = (4k + 4)/4 = k + 1，恰好等于 a/4 + 1（a/4=k.5，整数除法得 k，k+1=k+1）。 例：a=18（4×4+2）→ (18+2)/4=20/4=5，和 18/4+1=4+1=5 一致。 可以理解为偏移量 2 的作用是 “补齐” 到下一个能被 4 整除的数的一半，从而通过整数除法直接得到正确结果。

1054. 相邻字符判相等

描述:

输入一行字符（长度小于等于1000），判断其中是否存在相邻两个字符相同的情形，若有，则输出该相同的字符并结束程序(只需输出第一种相等的字符即可)。否则输出No。

输入:

输入一行字符（长度小于等于1000）

输出:

若有相邻字符相等则输出该相同的字符，否则输出No。（只需要输出第一种相同的情况即可）

例子:

输入:

1

hello anna

正确输出:

1

l

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <stdio.h>
#include <string.h>

int main() {
    char s ='�';
    char c;
    int count = 0;
    if (scanf("%c", &c) != 1) {
        printf("Non");
        return 0;
    }
    count++;
    while (count<1000&&scanf("%c", &c)==1) {
        if (c == 'n') {
            break;
        }
        if (c==s) {
            printf("%cn", c);
            return 0;
        }
        s=c;
        count++;
    }
    printf("Non");
    return 0;
}

解析：

运用最基础的while循环➕if判断语句 引入s作为临时空间存储上一个字符

1105. 求阶乘之和

描述:

求1!+2!+3!+…+n!的和。

输入:

输入一个正整数n（n≤12）。

输出:

输出1!+2!+3!+…+n!的值。

例子:

输入:

1

5

正确输出:

1

153

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13

#include <stdio.h>
int main() {
    int n;
    int sum =1;
    int num =0;
    scanf("%d", &n);
        for (int j=1;j<=n;j++) {
            sum *= j;
            num =num+sum;
    }
    printf("%d", num);
    return 0;
}

P1085 [NOIP 2004 普及组] 不高兴的津津

题目描述

津津上初中了。妈妈认为津津应该更加用功学习，所以津津除了上学之外，还要参加妈妈为她报名的各科复习班。另外每周妈妈还会送她去学习朗诵、舞蹈和钢琴。但是津津如果一天上课超过八个小时就会不高兴，而且上得越久就会越不高兴。假设津津不会因为其它事不高兴，并且她的不高兴不会持续到第二天。请你帮忙检查一下津津下周的日程安排，看看下周她会不会不高兴；如果会的话，哪天最不高兴。

输入格式

输入包括 7 行数据，分别表示周一到周日的日程安排。每行包括两个小于 10 的非负整数，用空格隔开，分别表示津津在学校上课的时间和妈妈安排她上课的时间。

输出格式

一个数字。如果不会不高兴则输出 0，如果会则输出最不高兴的是周几（用 1, 2, 3, 4, 5, 6, 7 分别表示周一，周二，周三，周四，周五，周六，周日）。如果有两天或两天以上不高兴的程度相当，则输出时间最靠前的一天。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7

5 3
6 2
7 2
5 3
5 4
0 4
0 6

输出 #1

1

3

说明/提示

NOIP2004 普及组第 1 题

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

#include <iostream>
using namespace std;

int main(){
    int max_time = 8, day = 0;
    for(int i = 1; i <= 7; i++){
        int t1, t2;
        cin >> t1 >> t2;
        int total = t1 + t2;

        if(total > max_time){
            max_time = total;
            day = i;
        }
    }
    cout << day;
    return 0;
}

详解：

这段代码主要运用了遍历 + 打擂台的算法思想。 核心思想解析：

• 遍历：通过 for 循环依次处理 7 天的数据
• 打擂台：
  • 用max_time记录当前找到的最大工作时间
  • 用day记录对应的日期
  • 每读取一天数据就比较，若超过当前最大值则更新

这种 “边遍历边更新最优解” 的模式是编程中非常基础且常用的方法，尤其适用于需要从一系列数据中找出最大值 / 最小值及其位置的场景。

辗转相除法

定义与原理

辗转相除法是求最大公约数（GCD, Greatest Common Divisor）的一种算法。其基本原理是：两个整数的最大公约数等于其中较小的数和两数相除的余数的最大公约数。具体公式为： gcd(a,b)=gcd(b,amod  b)

举例理解

比如现在要求这两个数 32，26的最大公约数，解法如下： 32/26=1…6 (此行除数26作下一行的被除数，余数作为除数) 26/6=4…2 (此行同理) 6/2=3…0 (此处余数为零，意味着最大公约数就是2) 反复把一个式子中的除数当作被除数去除余数，直到最后余数等于0。 最大公约数就是最后那个式子的除数，本例就是2。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

#include <stdio.h>
int main()
{
    int u, v;
    scanf("%d %d", &u, &v);
    while (v != 0)
    {
        int tmp = u % v;
        u = v;
        v = tmp;
    }
    printf("%d", u);
    return 0;

}

P1055 [NOIP 2008 普及组] ISBN 号码

题目描述

每一本正式出版的图书都有一个 ISBN 号码与之对应，ISBN 码包括 $9$ 位数字、$1$ 位识别码和 $3$ 位分隔符，其规定格式如 x-xxx-xxxxx-x，其中符号 - 就是分隔符（键盘上的减号），最后一位是识别码，例如 0-670-82162-4就是一个标准的 ISBN 码。ISBN 码的首位数字表示书籍的出版语言，例如 $0$ 代表英语；第一个分隔符 - 之后的三位数字代表出版社，例如 $670$ 代表维京出版社；第二个分隔符后的五位数字代表该书在该出版社的编号；最后一位为识别码。 识别码的计算方法如下： 首位数字乘以 $1$ 加上次位数字乘以 $2$ ……以此类推，用所得的结果 $ bmod 11$，所得的余数即为识别码，如果余数为 $10$，则识别码为大写字母 $X$。例如 ISBN 号码 0-670-82162-4 中的识别码 $4$ 是这样得到的：对 067082162 这$9$个数字，从左至右，分别乘以 $1,2,dots,9$ 再求和，即 $$ 0times 1+6times 2+……+2times 9=158 $$，然后取 $158 bmod 11$ 的结果 $4$ 作为识别码。 你的任务是编写程序判断输入的 ISBN 号码中识别码是否正确，如果正确，则仅输出 Right；如果错误，则输出你认为是正确的 ISBN 号码。

输入格式

一个字符序列，表示一本书的 ISBN 号码（保证输入符合 ISBN 号码的格式要求）。

输出格式

一行，假如输入的 ISBN 号码的识别码正确，那么输出 Right，否则，按照规定的格式，输出正确的 ISBN 号码（包括分隔符 -）。

输入输出样例 #1

输入 #1

1

0-670-82162-4

输出 #1

1

Right

输入输出样例 #2

输入 #2

1

0-670-82162-0

输出 #2

1

0-670-82162-4

说明/提示

2008 普及组第一题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#include <iostream>
#include <string> // 必须包含 string 头文件

int main() {
    std::string isbn_str;
    std::cin >> isbn_str; // 读取整个 ISBN 字符串，包括 '-'

    int sum = 0;
    int weight = 1;

    // 1. 计算前9个有效数字的加权和
    // 遍历字符串，跳过所有'-'，直到处理完9个数字
    for (char c : isbn_str) {
        if (c == '-') {
            continue; // 跳过分隔符
        }
        // 检查是否已经处理了9个数字
        if (weight > 9) {
            break;
        }
        // 将字符数字转为整数并计算
        sum += (c - '0') * weight;
        weight++;
    }

    // 2. 计算正确的识别码
    char correct_check;
    int remainder = sum % 11;
    if (remainder == 10) {
        correct_check = 'X';
    } else {
        correct_check = '0' + remainder; // 将整数转为字符
    }

    // 3. 获取用户输入的识别码（字符串的最后一个字符）
    char input_check = isbn_str.back();

    // 4. 比较并输出结果
    if (correct_check == input_check) {
        std::cout << "Right" << std::endl;
    } else {
        // 如果错误，替换字符串的最后一个字符并输出
        isbn_str.back() = correct_check;
        std::cout << isbn_str << std::endl;
    }

    return 0;
}

解析：

将字符数字转化为数字

在编程中，经常需要将字符类型的数字转换为整数类型的数字。 使用减去字符 ‘0’ 的方法 字符 ‘0’ 到 ‘9’ 的 ASCII 值分别是 48 到 57。因此，可以通过减去字符 ‘0’ 的 ASCII 值来将字符数字转换为整数。例如：

1
2
3
4
5
6
7

#将字符 '2' 转换为整数 2

char_digit = '2'

int_digit = ord(char_digit) - ord('0')

print(int

在 C 语言中，可以使用类似的方法：

1
2
3
4
5
6
7
8
9
10
11

char buf[4] = "123";

int num = 0;

for (int i = 0; i < strlen(buf); i++) {

num = num * 10 + buf[i] - '0'; // 通过减去 '0' 将字符转换为整数

}

printf("%dn", num); // 输出: 123

这种方法的原理是利用了字符 ‘0’ 到 ‘9’ 的 ASCII 值之间的差值。

P2669 [NOIP 2015 普及组] 金币

题目背景

NOIP2015 普及组 T1

题目描述

国王将金币作为工资，发放给忠诚的骑士。第一天，骑士收到一枚金币；之后两天（第二天和第三天），每天收到两枚金币；之后三天（第四、五、六天），每天收到三枚金币；之后四天（第七、八、九、十天），每天收到四枚金币……；这种工资发放模式会一直这样延续下去：当连续 $n$ 天每天收到 $n$ 枚金币后，骑士会在之后的连续 $n+1$ 天里，每天收到 $n+1$ 枚金币。 请计算在前 $k$ 天里，骑士一共获得了多少金币。

输入格式

一个正整数 $k$，表示发放金币的天数。

输出格式

一个正整数，即骑士收到的金币数。

输入输出样例 #1

输入 #1

1

6

输出 #1

1

14

输入输出样例 #2

输入 #2

1

1000

输出 #2

1

29820

说明/提示

【样例 1 说明】 骑士第一天收到一枚金币；第二天和第三天，每天收到两枚金币；第四、五、六天，每天收到三枚金币。因此一共收到 $1+2+2+3+3+3=14$ 枚金币。 对于 $100%$ 的数据，$1le kle 10^4$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <iostream>
using namespace std;

int main() {
    int k;                  // 总共要算多少天（输入的天数）
    cin >> k;               // 输入k（比如输入6）

    int total = 0;          // 记账本：总金币数（初始为0）
    int day_count = 0;      // 已算过的天数（初始为0，慢慢累加）
    int stage = 1;          // 当前要算的批次（从第1批开始）

    // 循环算账：直到已算的天数达到k天为止
    while (true) {
        // 先判断：当前批次的所有天，能不能全算进剩余的天数里？
        // 比如当前批次是3天，已算6天，k=6 → 6+3>6，不能全算；如果k=9，就能全算
        if (day_count + stage <= k) {
            // 情况1：能全算（完整批次）
            total += stage * stage;  // 该批次总金币=天数×每天金币（比如3批：3×3=9）
            day_count += stage;       // 已算天数增加（比如6+3=9）
            stage++;                  // 下一批次（比如3批之后算4批）
        } else {
            // 情况2：不能全算（不完整批次）
            int remain_day = k - day_count;  // 剩余没算的天数（比如k=7，已算6天 → 剩1天）
            total += remain_day * stage;     // 剩余天数的金币（1天×4枚=4枚）
            break;                          // 所有天算完了，退出循环
        }
    }

    cout << total << endl;  // 输出总金币（比如14）
    return 0;
}

P5723 【深基4.例13】质数口袋

题目描述

小 A 有一个质数口袋，里面可以装各个质数。他从 $2$ 开始，依次判断各个自然数是不是质数，如果是质数就会把这个数字装入口袋。 口袋的负载量就是口袋里的所有数字之和。 但是口袋的承重量有限，装的质数的和不能超过 $L$。给出 $L$，请问口袋里能装下几个质数？将这些质数从小往大输出，然后输出最多能装下的质数的个数，数字之间用换行隔开。

输入格式

一行一个正整数 $L$。

输出格式

将这些质数从小往大输出，然后输出最多能装下的质数个数。

输入输出样例 #1

输入 #1

1

100

输出 #1

1
2
3
4
5
6
7
8
9
10

2
3
5
7
11
13
17
19
23
9

输入输出样例 #2

输入 #2

1

5

输出 #2

1
2
3

2
3
2

输入输出样例 #3

输入 #3

1

11

输出 #3

1
2
3
4

2
3
5
3

说明/提示

数据保证，$1 le L le {10}^5$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

#include <iostream>
#include <cmath> // 为了使用 sqrt 函数
using namespace std;

// 函数：判断一个数是否为质数
// 质数是只能被 1 和它本身整除的大于 1 的自然数
bool is_prime(int num) {
    if (num <= 1) {
        return false; // 1 和小于 1 的数都不是质数
    }
    // 一个优化：只需检查到 sqrt(num) 即可
    // 如果 num 有一个因子大于它的平方根，那么另一个因子必然小于它的平方根
    for (int i = 2; i <= sqrt(num); ++i) {
        if (num % i == 0) {
            // 如果能被 i 整除，说明不是质数
            return false;
        }
    }
    return true; // 循环结束都没有找到因子，说明是质数
}

int main() {
    // 提高C++ IO效率 (可选，但在竞赛中是好习惯)
    std::ios_base::sync_with_stdio(false);
    std::cin.tie(NULL);

    int L;
    std::cin >> L;

    int sum = 0;       // 口袋里质数的总和，初始为0
    int count = 0;     // 口袋里质数的个数，初始为0
    int current_num = 2; // 从2开始检查，因为2是最小的质数

    // 循环：只要当前数不超过 L，就一直尝试
    // （一个优化：如果 current_num 本身就比 L 大，那肯定装不下）
    while (current_num <= L) {
        // 步骤1：判断 current_num 是不是质数
        if (is_prime(current_num)) {
            // 步骤2：判断装入口袋后总和是否超过 L
            if (sum + current_num <= L) {
                // 如果没超过，就装进去
                sum += current_num;
                count++;
                // 题目要求：将这些质数从小往大输出
                std::cout << current_num << std::endl;
            } else {
                // 如果超过了，说明口袋满了，后面的质数更大，肯定也装不下
                // 直接跳出循环
                break;
            }
        }
        // 检查下一个数
        current_num++;
    }

    // 最后，输出最多能装下的质数的个数
    std::cout << count << std::endl;

    return 0;
}

P1217 [USACO1.5] 回文质数 Prime Palindromes

题目描述

因为 $151$ 既是一个质数又是一个回文数（从左到右和从右到左是看一样的），所以 $151$ 是回文质数。 写一个程序来找出范围 $[a,b] (5 le a < b le 100,000,000)$（一亿）间的所有回文质数。

输入格式

第一行输入两个正整数 $a$ 和 $b$。

输出格式

输出一个回文质数的列表，一行一个。

输入输出样例 #1

输入 #1

1

5 500

输出 #1

1
2
3
4
5
6
7
8
9
10
11
12

5
7
11
101
131
151
181
191
313
353
373
383

说明/提示

Hint 1: Generate the palindromes and see if they are prime. 提示 1: 找出所有的回文数再判断它们是不是质数（素数）. Hint 2: Generate palindromes by combining digits properly. You might need more than one of the loops like below. 提示 2: 要产生正确的回文数，你可能需要几个像下面这样的循环。 题目翻译来自NOCOW。 USACO Training Section 1.5 产生长度为 $5$ 的回文数：

1
2
3
4
5
6
7

for (d1 = 1; d1 <= 9; d1+=2) {    // 只有奇数才会是素数
     for (d2 = 0; d2 <= 9; d2++) {
         for (d3 = 0; d3 <= 9; d3++) {
           palindrome = 10000*d1 + 1000*d2 +100*d3 + 10*d2 + d1;//(处理回文数...)
         }
     }
 }

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

#include <iostream>
#include <cmath>
using namespace std;

// 判断一个数是否为质数
bool is_prime(int num) {
    if (num < 2) return false;
    if (num == 2) return true;
    if (num % 2 == 0) return false; // 偶数直接排除
    // 只遍历奇数，减少循环次数
    for (int i = 3; i <= sqrt(num); i += 2) {
        if (num % i == 0) return false;
    }
    return true;
}

// 生成所有在[a,b]区间内的回文数，并判断是否为质数，符合条件则输出
void generate_palindromes(int a, int b) {
    // 1. 生成1位回文数（5、7，因为题目a≥5）
    int one_digit[] = {5, 7};
    for (int p : one_digit) {
        if (p >= a && p <= b) {
            cout << p << endl;
        }
    }

    // 2. 生成3位回文数（格式：d1 d2 d1，d1为奇数，d2任意）
    for (int d1 = 1; d1 <= 9; d1 += 2) { // d1：1、3、5、7、9（首位/末位）
        for (int d2 = 0; d2 <= 9; d2++) { // d2：中间位
            int p = d1 * 100 + d2 * 10 + d1;
            if (p >= a && p <= b && is_prime(p)) {
                cout << p << endl;
            }
        }
    }

    // 3. 生成5位回文数（格式：d1 d2 d3 d2 d1）
    for (int d1 = 1; d1 <= 9; d1 += 2) {
        for (int d2 = 0; d2 <= 9; d2++) {
            for (int d3 = 0; d3 <= 9; d3++) {
                int p = d1 * 10000 + d2 * 1000 + d3 * 100 + d2 * 10 + d1;
                if (p >= a && p <= b && is_prime(p)) {
                    cout << p << endl;
                }
            }
        }
    }

    // 4. 生成7位回文数（格式：d1 d2 d3 d4 d3 d2 d1）
    for (int d1 = 1; d1 <= 9; d1 += 2) {
        for (int d2 = 0; d2 <= 9; d2++) {
            for (int d3 = 0; d3 <= 9; d3++) {
                for (int d4 = 0; d4 <= 9; d4++) {
                    int p = d1 * 1000000 + d2 * 100000 + d3 * 10000 + d4 * 1000 + d3 * 100 + d2 * 10 + d1;
                    if (p >= a && p <= b && is_prime(p)) {
                        cout << p << endl;
                    }
                }
            }
        }
    }
}

int main() {
    int a, b;
    cin >> a >> b;
    generate_palindromes(a, b);
    return 0;
}

知识：

1. 先学 11 的整除判定规则

一个数能否被 11 整除，只需计算：“奇数位数字之和” 与 “偶数位数字之和” 的差值（大减小）。若差值能被 11 整除（包括差值为 0），则这个数能被 11 整除。 例如1234 奇数位和=1+3 偶数位和=2+4

2. 用偶数位回文数验证规律

以最典型的 “4 位回文数（d1d2d2d1）” 和 “6 位回文数（d1d2d3d3d2d1）” 为例：

• 4 位回文数（d1d2d2d1）：
  • 从右数，奇数位（1、3 位）：d1 + d2
  • 从右数，偶数位（2、4 位）：d2 + d1
  • 差值：(d1+d2) - (d2+d1) = 0，0 能被 11 整除 → 4 位回文数必能被 11 整除（如 1221÷11=111，2332÷11=212）。
• 6 位回文数（d1d2d3d3d2d1）：
  • 从右数，奇数位（1、3、5 位）：d1 + d3 + d2
  • 从右数，偶数位（2、4、6 位）：d2 + d3 + d1
  • 差值：0，同样能被 11 整除 → 6 位回文数必能被 11 整除（如 123321÷11=11211）。

3. 结论：偶数位回文数全是 “非质数”

除了 2 位回文数中的 11（唯一的偶数位回文质数），其他所有偶数位回文数（2 位的 22、33…，4 位、6 位、8 位）都能被 11 整除，且结果大于 1，因此不符合质数定义。

三、为什么只遍历 3、5、7 位回文数？

因为这三类回文数是 “奇数位回文数”，且在题目范围（5≤a<b≤1 亿）内，有可能是质数，具体原因如下：

1. 1 位回文数：虽然也是奇数位，但只有 5、7 两个质数（1、3 小于题目中 a 的最小值 5，9 不是质数），代码中通常单独处理（如之前的代码直接列举 5、7），无需循环构造。
2. 3 位回文数：范围 101-999，奇数位，不会必被 11 整除，存在大量质数（如 101、131）。
3. 5 位回文数：范围 10001-99999，奇数位，存在质数（如 10007、10031）。
4. 7 位回文数：范围 1000001-9999999，奇数位，存在质数（如 1000003、1000033）。
5. 9 位回文数：最小是 100000001，已超过 1 亿（题目中 b 的最大值），不在处理范围内。

简单说：3、5、7 位回文数是题目范围内 “唯一可能是质数的回文数类型”，遍历它们就能覆盖所有答案，避免做无用功。

P1307 [NOIP 2011 普及组] 数字反转

题目描述

给定一个整数 $N$，请将该数各个位上数字反转得到一个新数。新数也应满足整数的常见形式，即除非给定的原数为零，否则反转后得到的新数的最高位数字不应为零（参见样例 2）。

输入格式

一个整数 $N$。

输出格式

一个整数，表示反转后的新数。

输入输出样例 #1

输入 #1

1

123

输出 #1

1

321

输入输出样例 #2

输入 #2

1

-380

输出 #2

1

-83

说明/提示

【数据范围】 $-1,000,000,000leq Nleq 1,000,000,000 $。 noip2011 普及组第一题

代码：

我的代码（臃肿）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

#include<iostream>
#include<vector>
using namespace std;
int main() {
    int n;
    cin>>n;
    vector<int> v;
    if (n == 0) {
        cout << 0 << endl;
        return 0;
    }
    if (n<=0) {
        n=-n;
        while(n!=0) {
            v.push_back(n%10);
            n=n/10;
        }
        if (v[0]==0) {
            cout<<"-";
            int startIndex = 0;
            while (startIndex < v.size() && v[startIndex] == 0) {
                startIndex++;
            }
            for(int i =startIndex;i<=v.size()-1;i++) {
                cout<<v[i];
            }
        }else {
            cout<<"-";
            int startIndex = 0;
            while (startIndex < v.size() && v[startIndex] == 0) {
                startIndex++;
            }
            for(int i=startIndex;i<=v.size()-1;i++) {
                cout<<v[i];
            }
        }
    }else{ while(n!=0) {
        v.push_back(n%10);
        n=n/10;
    }
        if (v[0]==0) {
            int startIndex = 0;
            while (startIndex < v.size() && v[startIndex] == 0) {
                startIndex++;
            }
            for(int i=startIndex;i<=v.size()-1;i++) {
                cout<<v[i];
            }
        }else {
            int startIndex = 0;
            while (startIndex < v.size() && v[startIndex] == 0) {
                startIndex++;
            }
            for(int i=startIndex;i<=v.size()-1;i++) {
                cout<<v[i];
            }
        }
    }

    return 0;
}

优化代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#include <iostream>
using namespace std;

int main() {
    long long n;
    cin >> n;

    // 处理负数情况
    if (n < 0) {
        cout << "-";
        n = -n;
    }

    long long reversed = 0;
    while (n > 0) {
        // 取出最后一位数字，添加到反转数的末尾
        reversed = reversed * 10 + n % 10;
        n /= 10;
    }

    cout << reversed << endl;
    return 0;
}

P1420 最长连号

题目描述

输入长度为 $n$ 的一个正整数序列，要求输出序列中最长连号的长度。 连号指在序列中，从小到大的连续自然数。

输入格式

第一行，一个整数 $n$。 第二行，$n$ 个整数 $a_i$，之间用空格隔开。

输出格式

一个数，最长连号的个数。

输入输出样例 #1

输入 #1

1
2

10
1 5 6 2 3 4 5 6 8 9

输出 #1

1

5

说明/提示

数据规模与约定

对于 $100%$ 的数据，保证 $1 leq n leq 10^4$，$1 leq a_i leq 10^9$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    int num1,num2,current_len=1,max_len=1;
    cin>> num1;
    for(int i=1;i<n;i++) {
        cin>> num2;
        if(num2==num1+1) {
            current_len++;
            if (current_len>max_len) {
                max_len =current_len;
            }
        }else {
            current_len=1;
        }
        num1=num2;
    }
    cout << max_len << endl;
    return 0;
}

P1075 [NOIP 2012 普及组] 质因数分解

题目描述

已知正整数 $n$ 是两个不同的质数的乘积，试求出两者中较大的那个质数。

输入格式

输入一个正整数 $n$。

输出格式

输出一个正整数 $p$，即较大的那个质数。

输入输出样例 #1

输入 #1

1

21

输出 #1

1

7

说明/提示

$1 le nle 2times 10^9$ NOIP 2012 普及组 第一题

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;

    // 特殊情况：n<=1没有质因数
    if (n <= 1) {
        cout << "无质因数" << endl;
        return 0;
    }

    int max_prime = 0;
    // 第一步：先除以所有2的倍数（处理最小质因数2）
    while (n % 2 == 0) {
        max_prime = 2; // 2是当前质因数
        n /= 2;        // 除以2，缩小n
    }

    // 第二步：处理奇数因数（从3开始，每次+2，避免偶数）
    // 此时n已为奇数，只需遍历到sqrt(n)即可
    for (int i = 3; i * i <= n; i += 2) {
        while (n % i == 0) {
            max_prime = i; // i是当前质因数
            n /= i;        // 除以i，缩小n
        }
    }

    // 第三步：如果最后剩下的n>2，说明它本身是质数（最大质因数）
    if (n > 2) {
        max_prime = n;
    }

    cout << max_prime << endl;
    return 0;
}

P1914 小书童——凯撒密码

题目背景

某蒟蒻迷上了 “小书童”，有一天登陆时忘记密码了（他没绑定邮箱 or 手机），于是便把问题抛给了神犇你。

题目描述

蒟蒻虽然忘记密码，但他还记得密码是由一个字符串组成。密码是由原文字符串（由不超过 50 个小写字母组成）中每个字母向后移动 $n$ 位形成的。z 的下一个字母是 a，如此循环。他现在找到了移动前的原文字符串及 $n$，请你求出密码。

输入格式

第一行：$n$。第二行：未移动前的一串字母。

输出格式

一行，是此蒟蒻的密码。

输入输出样例 #1

输入 #1

1
2

1
qwe

输出 #1

1

rxf

说明/提示

字符串长度 $le 50$，$1 leq n leq 26$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

#include <iostream>
using namespace std;
int main() {
    int n;
    cin >> n;
    string s;
    cin >> s;
    for (int i = 0; i < s.size(); i++) {
        s[i]=(s[i] -'a'+n)%26+'a';
    }
    cout << s << endl;
    return 0;

}

P1957 口算练习题

题目描述

王老师正在教简单算术运算。细心的王老师收集了 $i$ 道学生经常做错的口算题，并且想整理编写成一份练习。编排这些题目是一件繁琐的事情，为此他想用计算机程序来提高工作效率。王老师希望尽量减少输入的工作量，比如 $texttt{5+8}$ 的算式最好只要输入 $texttt 5$ 和 $texttt 8$，输出的结果要尽量详细以方便后期排版的使用，比如对于上述输入进行处理后输出 $texttt{5+8=13}$ 以及该算式的总长度 $6$。王老师把这个光荣的任务交给你，请你帮他编程实现以上功能。

输入格式

第一行一个整数 $i$。 接着的 $i$ 行为需要输入的算式，每行可能有三个数据或两个数据。 若该行为三个数据则第一个数据表示运算类型，$texttt a$ 表示加法运算，$texttt b$ 表示减法运算，$texttt c$ 表示乘法运算，接着的两个数据表示参加运算的运算数。 若该行为两个数据，则表示本题的运算类型与上一题的运算类型相同，而这两个数据为运算数。

输出格式

输出 $2times i$ 行。对于每个输入的算式，输出完整的运算式及结果，第二行输出该运算式的总长度。

输入输出样例 #1

输入 #1

1
2
3
4
5

4
a 64 46
275 125
c 11 99
b 46 64

输出 #1

1
2
3
4
5
6
7
8

64+46=110
9
275+125=400
11
11*99=1089
10
46-64=-18
9

说明/提示

【数据规模与约定】

对于 $50%$ 的数据，输入的算式都有三个数据。 对于所有数据，$0<ileq 50$，第一个算式一定有三个数据，运算数为非负整数且小于 $10000$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int main(){
    int i;
    char s[10000],b[10];
    int m,n,a;
    char c;
    cin>>i;
    for(int j=0;j<i;j++) {
        cin>>b;
        if (b[0]>='a' && b[0]<='z') {
            c =b[0];
            cin>>m>>n;
        }else {
            sscanf(b,"%d",&m);
            cin>>n;
        }
        memset(s,0,sizeof(s));
        if (c =='a') {
            sprintf(s,"%d+%d=%d",m,n,m+n);
        }else if (c=='b') {
            sprintf(s,"%d-%d=%d",m,n,m-n);
        }else if (c=='c') {
            sprintf(s,"%d*%d=%d",m,n,m*n);
        }
        cout<<s<<endl<<strlen(s)<<endl;
    }
    return 0;
}

P5461 赦免战俘

题目背景

借助反作弊系统，一些在月赛有抄袭作弊行为的选手被抓出来了！

题目描述

现有 $2^ntimes 2^n (nle10)$ 名作弊者站成一个正方形方阵等候 kkksc03 的发落。kkksc03 决定赦免一些作弊者。他将正方形矩阵均分为 4 个更小的正方形矩阵，每个更小的矩阵的边长是原矩阵的一半。其中左上角那一个矩阵的所有作弊者都将得到赦免，剩下 3 个小矩阵中，每一个矩阵继续分为 4 个更小的矩阵，然后通过同样的方式赦免作弊者……直到矩阵无法再分下去为止。所有没有被赦免的作弊者都将被处以棕名处罚。 给出 $n$，请输出每名作弊者的命运，其中 0 代表被赦免，1 代表不被赦免。

输入格式

一个整数 $n$。

输出格式

$2^n times 2^n$ 的 01 矩阵，代表每个人是否被赦免。数字之间有一个空格。

输入输出样例 #1

输入 #1

1

3

输出 #1

1
2
3
4
5
6
7
8

0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 1
0 0 0 0 0 1 0 1
0 0 0 0 1 1 1 1
0 0 0 1 0 0 0 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
1 1 1 1 1 1 1 1

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

void solve(vector<vector<int>>& grid, int x, int y, int size) {
    if (size == 1) {
        return;
    }

    int half = size / 2;

    // 赦免左上角矩阵
    for (int i = x; i < x + half; i++) {
        for (int j = y; j < y + half; j++) {
            grid[i][j] = 0;
        }
    }
    //
    // 递归处理其余三个矩阵
    solve(grid, x, y + half, half);
    solve(grid, x + half, y, half);
    solve(grid, x + half, y + half, half);
}

int main() {
    int n;
    cin >> n;

    int size = pow(2, n);
    vector<vector<int>> grid(size, vector<int>(size, 1));

    solve(grid, 0, 0, size);

    // 输出结果
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            cout << grid[i][j];
            if (j < size - 1) {
                cout << " ";
            }
        }
        cout << endl;
    }

    return 0;
}